geo-htseq-paper/README.md

Working with model objects

Install

• Download and install R https://www.r-project.org (and RStudio https://www.rstudio.com/products/rstudio/).

• Go to R console or open scripts/README.Rmd in RStudio.

• Install these packages (this needs to be done once).

if(!require(brms)){
  install.packages(c("brms", "here"))
  library(brms)
  library(here)
}

## Loading required package: brms

## Loading required package: Rcpp

## Loading 'brms' package (version 2.14.4). Useful instructions
## can be found by typing help('brms'). A more detailed introduction
## to the package is available through vignette('brms_overview').

## 
## Attaching package: 'brms'

## The following object is masked from 'package:stats':
## 
##     ar

Run

In R console OR in .Rmd file:

• Load packages to R environment.

library(brms)
library(here)

• Load the model object and print model summary.

m <- readRDS(here("models/anticons_detool.rds"))
print(m)

##  Family: bernoulli 
##   Links: mu = logit 
## Formula: anticons ~ de_tool 
##    Data: data (Number of observations: 2109) 
## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
##          total post-warmup samples = 4000
## 
## Population-Level Effects: 
##                Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept         -3.51      0.23    -4.00    -3.09 1.00      942     1128
## de_tooldeseq       2.66      0.25     2.19     3.18 1.00     1080     1153
## de_tooledger       3.57      0.26     3.07     4.10 1.00     1051     1435
## de_toollimma       3.58      0.42     2.77     4.42 1.00     1693     2093
## de_toolunknown     2.46      0.25     1.99     2.98 1.00     1052     1153
## 
## Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).

• Get fitted coefficients with 95% credible intervals.

posterior_summary(m)

##                     Estimate Est.Error        Q2.5       Q97.5
## b_Intercept        -3.514582 0.2300317   -4.001753   -3.088126
## b_de_tooldeseq      2.656732 0.2492621    2.188271    3.183202
## b_de_tooledger      3.571890 0.2642955    3.074863    4.103799
## b_de_toollimma      3.579595 0.4163380    2.773039    4.424586
## b_de_toolunknown    2.461885 0.2476724    1.990004    2.975438
## lp__             -969.443536 1.6153116 -973.461001 -967.323674

• Get the full posterior.

post <- posterior_samples(m)
head(post)

##   b_Intercept b_de_tooldeseq b_de_tooledger b_de_toollimma b_de_toolunknown      lp__
## 1   -3.300792       2.355140       3.418613       3.433826         2.191998 -968.0241
## 2   -3.485360       2.606697       3.559653       3.530865         2.329601 -967.5360
## 3   -3.628822       2.705505       3.763745       3.932852         2.560540 -967.7857
## 4   -3.621123       2.917484       3.643992       3.647139         2.545874 -968.5439
## 5   -3.795040       2.929855       3.797475       3.520305         2.633857 -968.9733
## 6   -3.248306       2.532679       3.443725       3.528865         2.130235 -969.7214

• What is the estimated difference in the proportion of anti-conservative p value histograms between DESeq2 and EdgeR?

posterior_deseq_edger <- inv_logit_scaled(post$b_de_tooldeseq - post$b_de_tooledger)
hist(posterior_deseq_edger, breaks = 40)

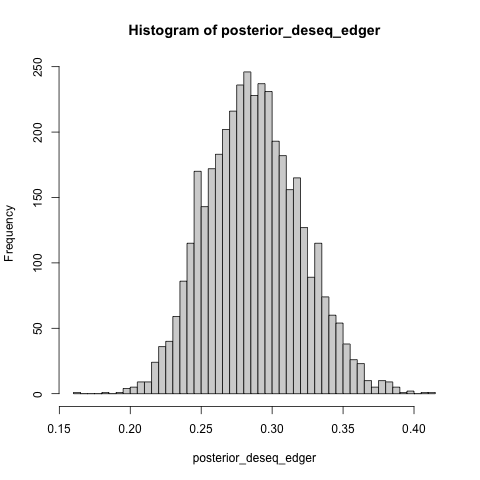
• The posterior summary for the effect size.

posterior_summary(posterior_deseq_edger) 

##       Estimate  Est.Error      Q2.5     Q97.5
## [1,] 0.2870903 0.03315653 0.2267546 0.3541821

The estimated effect size is somewhere between 22.7 and 35.4 percentage points.

• Get data from model object.

data <- m$data
head(data)

##   anticons  de_tool
## 1        1  unknown
## 2        0  unknown
## 3        1    edger
## 4        0 cuffdiff
## 5        0    limma
## 6        0  unknown

• Extract stan code from model object. This is the fullest model description.

stancode(m)

## // generated with brms 2.15.0
## functions {
## }
## data {
##   int<lower=1> N;  // total number of observations
##   int Y[N];  // response variable
##   int<lower=1> K;  // number of population-level effects
##   matrix[N, K] X;  // population-level design matrix
##   int prior_only;  // should the likelihood be ignored?
## }
## transformed data {
##   int Kc = K - 1;
##   matrix[N, Kc] Xc;  // centered version of X without an intercept
##   vector[Kc] means_X;  // column means of X before centering
##   for (i in 2:K) {
##     means_X[i - 1] = mean(X[, i]);
##     Xc[, i - 1] = X[, i] - means_X[i - 1];
##   }
## }
## parameters {
##   vector[Kc] b;  // population-level effects
##   real Intercept;  // temporary intercept for centered predictors
## }
## transformed parameters {
## }
## model {
##   // likelihood including constants
##   if (!prior_only) {
##     target += bernoulli_logit_glm_lpmf(Y | Xc, Intercept, b);
##   }
##   // priors including constants
##   target += student_t_lpdf(Intercept | 3, 0, 2.5);
## }
## generated quantities {
##   // actual population-level intercept
##   real b_Intercept = Intercept - dot_product(means_X, b);
## }

This document

This README.md was generated by running:

rmarkdown::render("scripts/README.Rmd", output_file = here::here("README.md"))