|
|
@@ -0,0 +1,675 @@
|
|
|
+---
|
|
|
+title: "Data Analysis of Predictive coding in ASD"
|
|
|
+author: "Z. Shi, L. Theisinger, F. Allenmark, R. Pistorius, H. Müller, C. Falter-Wagner"
|
|
|
+output: html_notebook
|
|
|
+---
|
|
|
+
|
|
|
+# Data Structure
|
|
|
+
|
|
|
+1. `/experiments`: Experimental codes and instructions
|
|
|
+
|
|
|
+This sub-folder contains Matlab codes and instructions for the duration reproduction task. The sequences of the duration reproductions are stored in the sub-folder `/experiments/seqs`. Those sequences were used for matched participants.
|
|
|
+
|
|
|
+2. `/data`: raw data files
|
|
|
+
|
|
|
+- `rawdata.csv`: Raw reproduction trials
|
|
|
+- `outliers.csv`: those produced almost flat reproduction
|
|
|
+
|
|
|
+3. `/figures`: store figures used in the paper.
|
|
|
+
|
|
|
+# Data Analysis
|
|
|
+
|
|
|
+## 1. load raw data
|
|
|
+```{r packages, message=FALSE, warning=FALSE, include=FALSE}
|
|
|
+# load packages
|
|
|
+library(tidyverse)
|
|
|
+library(ez)
|
|
|
+library(cowplot)
|
|
|
+library(BayesFactor) # in case need Bayes factor analysis
|
|
|
+library(bayestestR)
|
|
|
+library(rstatix) # using tidyverse friendly statistics
|
|
|
+library(GGally)
|
|
|
+
|
|
|
+# ---- read data and preparation -----
|
|
|
+rawdata = read_csv('./data/rawdata.csv')
|
|
|
+rawdata$group = toupper(rawdata$group)
|
|
|
+# flag
|
|
|
+saveFig = FALSE
|
|
|
+```
|
|
|
+
|
|
|
+Show the raw trial structure:
|
|
|
+```{r raw trial structure}
|
|
|
+glimpse(rawdata)
|
|
|
+
|
|
|
+```
|
|
|
+In the raw trials, there are several important columns which are relevant for further analyses.
|
|
|
+
|
|
|
+- `Duration`: The test durations generated by computer. 'pdur' is the actual presented durations by the computer. There were some fluctuations, but within 5 ms (within 1 refresh frame).
|
|
|
+- `sub`, `group`, `sequence` are anonymized subject number, group and the duration sequence used in the experiment.
|
|
|
+- `Reproduction`, `rep_err`: the reproduced durations and the reproduction errors compared to the given duration.
|
|
|
+- `itd`, `preDuration`: the inter-trial difference in a given trial, and the duration used in the previous trial. These were used in the sequential effect analysis.
|
|
|
+
|
|
|
+### Participants
|
|
|
+
|
|
|
+```{r participants}
|
|
|
+# Total participants
|
|
|
+print(length (unique(rawdata$sub)))
|
|
|
+# total sequences (pairs)
|
|
|
+print(length(unique(rawdata$sequence)))
|
|
|
+```
|
|
|
+
|
|
|
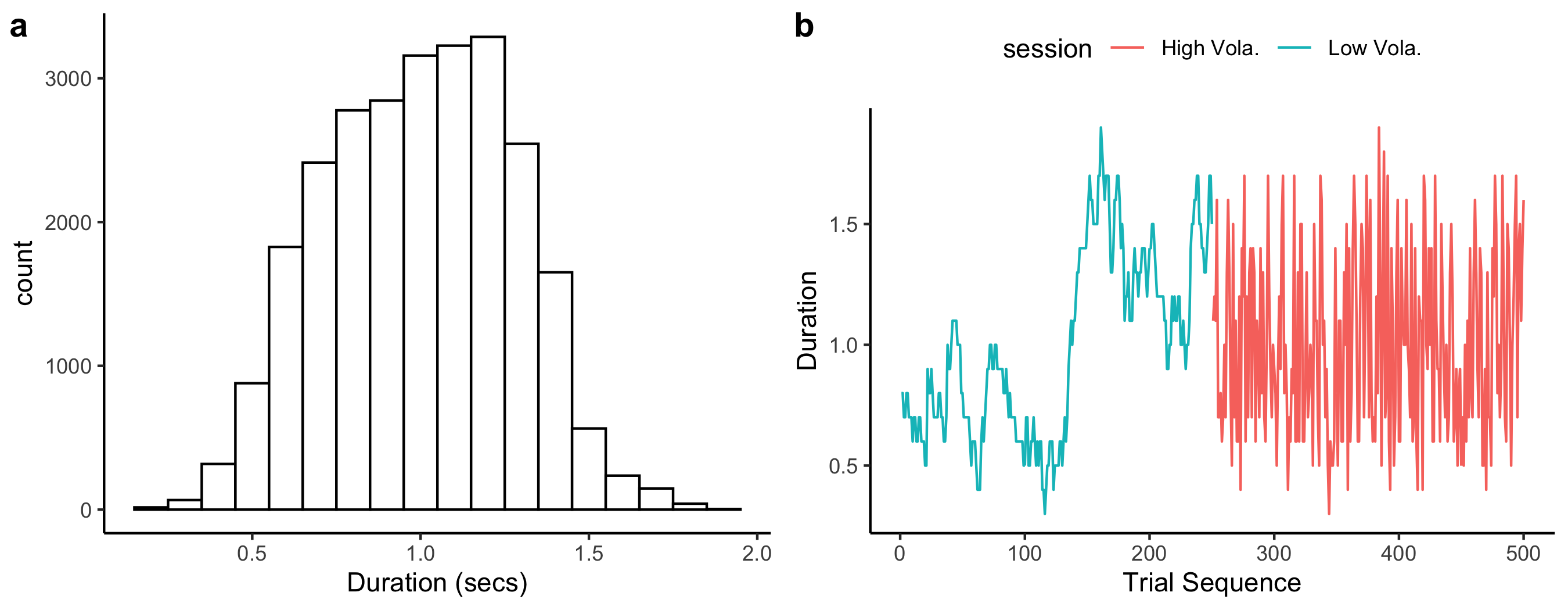
+## The sampled durations and sequences
|
|
|
+
|
|
|
+Let's first illustrate the sequence and the distribution of the sample durations.
|
|
|
+
|
|
|
+```{r sequence}
|
|
|
+# ---- illustrate one sequence -----
|
|
|
+fig11 = ggplot(rawdata, aes(Duration)) + geom_histogram(binwidth = 0.1, fill = I("white"), col = I('black')) +
|
|
|
+ theme_classic() + xlab('Duration (secs)')
|
|
|
+
|
|
|
+# a typical sequence
|
|
|
+sub1 = rawdata %>% filter(sub == 'ara27')
|
|
|
+fig12 = ggplot(sub1, aes(trlNo, Duration, color = Volatility)) + geom_line() +
|
|
|
+ xlab("Trial Sequence") + theme_classic()+
|
|
|
+ theme(legend.position = 'top')
|
|
|
+
|
|
|
+# histogram of the typical sequence
|
|
|
+
|
|
|
+fig13 = ggplot(sub1, aes(y=Duration, color = Volatility)) + geom_density() + theme_classic() + theme(legend.position = 'top')
|
|
|
+fig13
|
|
|
+
|
|
|
+fig1 = plot_grid(fig12,fig13, rel_widths =c(3,1))
|
|
|
+fig1
|
|
|
+if (saveFig){
|
|
|
+ ggsave("figures/fig_sequence.png", fig1, width=4, height=3.5)
|
|
|
+ ggsave("figures/fig_sequence.pdf", fig1, width=4, height=3.5)
|
|
|
+}
|
|
|
+```
|
|
|
+
|
|
|
+
|
|
|
+## Explorative data analysis and outlier detection
|
|
|
+
|
|
|
+We first estimate two key signatures - the central tendency index (ci) and the sequential dependence index (si).
|
|
|
+
|
|
|
+```{r linear_models}
|
|
|
+# using error for regression, -slope is the central tendency index.
|
|
|
+ct_model <- function(df){
|
|
|
+ lm(rep_err ~ Duration, data = df)
|
|
|
+}
|
|
|
+
|
|
|
+# sequential effect using the duration from the previous trial
|
|
|
+seq_model <- function(df){
|
|
|
+ lm(rep_err ~ preDuration, data = df)
|
|
|
+}
|
|
|
+
|
|
|
+# exclude extreme trials (beyond [1/3D, 3D])
|
|
|
+vdata = rawdata %>%
|
|
|
+ filter(Reproduction > Duration/3, Reproduction < 3*Duration)
|
|
|
+
|
|
|
+# calculate slope for the central tendency as well as the sequential dependence.
|
|
|
+slopes_ct <- vdata %>% group_by(sub, sequence, Volatility, group, Order) %>%
|
|
|
+ nest() %>% # nested data
|
|
|
+ mutate(model = map(data, ct_model)) %>% # linear regression
|
|
|
+ mutate(slope = map(model, broom::tidy)) %>% # get estimates out
|
|
|
+ unnest(slope, .drop = TRUE) %>% # remove raw data
|
|
|
+ select(-std.error,-statistic, -p.value) %>% # remove unnecessary columns
|
|
|
+ spread(term, estimate) %>% # spread estimates
|
|
|
+ rename(intercept_ct = `(Intercept)`, slope = Duration) %>%
|
|
|
+ select(-data, -model)
|
|
|
+
|
|
|
+#sequential effect
|
|
|
+slopes_seq <- vdata %>% filter(!is.na(preDuration)) %>%
|
|
|
+ group_by(sub, sequence, Volatility, group, Order) %>%
|
|
|
+ nest() %>% # nested data
|
|
|
+ mutate(model = map(data, seq_model)) %>% # linear regression
|
|
|
+ mutate(slope = map(model, broom::tidy)) %>% # get estimates out
|
|
|
+ unnest(slope, .drop = TRUE) %>% # remove raw data
|
|
|
+ select(-std.error,-statistic, -p.value) %>% # remove unnecessary columns
|
|
|
+ spread(term, estimate) %>% # spread estimates
|
|
|
+ rename(intercept_seq = `(Intercept)`, seq_slope = preDuration) %>%
|
|
|
+ select(-data, -model)
|
|
|
+
|
|
|
+# merge two tables together
|
|
|
+slopes_all = left_join(slopes_ct, slopes_seq,
|
|
|
+ by = c("sub", "sequence", "Volatility","group","Order")) %>%
|
|
|
+ mutate(ci = -slope, si = seq_slope) #central tendency index
|
|
|
+
|
|
|
+# estimated general biases (over-/under-estimates)
|
|
|
+
|
|
|
+# individual mean interval (middle point): most of them were around 1 by design
|
|
|
+mInterval = vdata %>% group_by(sub) %>% summarise(mDur = mean(Duration))
|
|
|
+
|
|
|
+# join the mean interval, and estimate the general bias
|
|
|
+slopes = slopes_all %>% left_join(., mInterval, by = c('sub')) %>%
|
|
|
+ mutate(gBias = (intercept_ct + slope * mDur)*1000)
|
|
|
+
|
|
|
+# change factor order for plotting
|
|
|
+slopes$Volatility = factor(slopes$Volatility)
|
|
|
+slopes$Order = factor(slopes$Order)
|
|
|
+slopes$group = factor(slopes$group)
|
|
|
+
|
|
|
+head(slopes)
|
|
|
+```
|
|
|
+
|
|
|
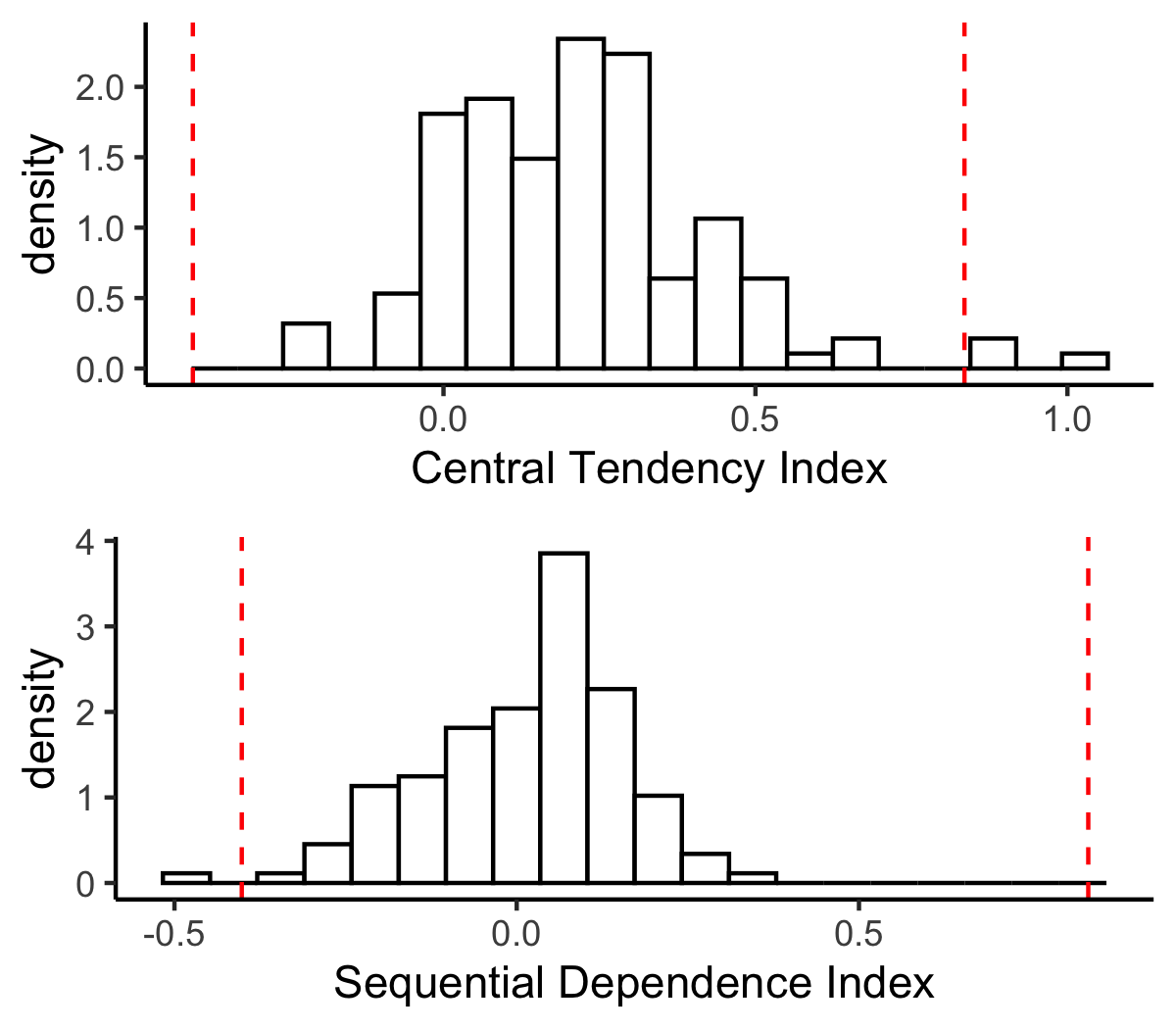
+Let's plot the histograms of the central tendency index and the sequential dependence index, which show some outliers. We visualize the outliers using 3-sigma rule. The 3-sigma rule only rule out 0.3% of the population if we assume the population is normal.
|
|
|
+
|
|
|
+```{r}
|
|
|
+ci_3sig = mean(slopes$ci) + c(-1,1)*3*sd(slopes$ci)
|
|
|
+si_3sig = mean(slopes$si) + c(-1,1)*3*sd(slopes$si)
|
|
|
+
|
|
|
+hist1 = ggplot(slopes, aes(x = ci, y = ..density..)) +
|
|
|
+ geom_histogram(colour = 1, fill = 'white', bins = 20) +
|
|
|
+ geom_vline(xintercept = ci_3sig, linetype = 'dashed', color = 'red') +
|
|
|
+ theme_classic() + xlab('Central Tendency Index')
|
|
|
+hist2 = ggplot(slopes, aes(x = si, y = ..density..)) +
|
|
|
+ geom_histogram(colour = 1, fill = 'white', bins = 20) +
|
|
|
+ geom_vline(xintercept = ci_3sig, linetype = 'dashed', color = 'red') +
|
|
|
+ theme_classic() + xlab('Sequential Dependence Index')
|
|
|
+
|
|
|
+hist_fig = plot_grid(hist1,hist2, nrow = 2)
|
|
|
+hist_fig
|
|
|
+if (saveFig){
|
|
|
+ ggsave("figures/hist_fig.png", hist_fig, width=4, height=3.5)
|
|
|
+ ggsave("figures/hist_fig.pdf", fig1, width=4, height=3.5)
|
|
|
+}
|
|
|
+
|
|
|
+```
|
|
|
+
|
|
|
+Note, the above outlier detection method is agnostic to the groups and conditions!
|
|
|
+
|
|
|
+Let's find out those outliers and exclude by sequences for further analyses (given that ASD and TD groups were paired).
|
|
|
+
|
|
|
+```{r}
|
|
|
+slopes %>% ungroup() %>% filter(ci > ci_3sig[2] | ci < ci_3sig[1] | si > si_3sig[2] | si < si_3sig[1]) %>% select(sequence) -> outlier_seq
|
|
|
+outlier_seq$sequence
|
|
|
+```
|
|
|
+
|
|
|
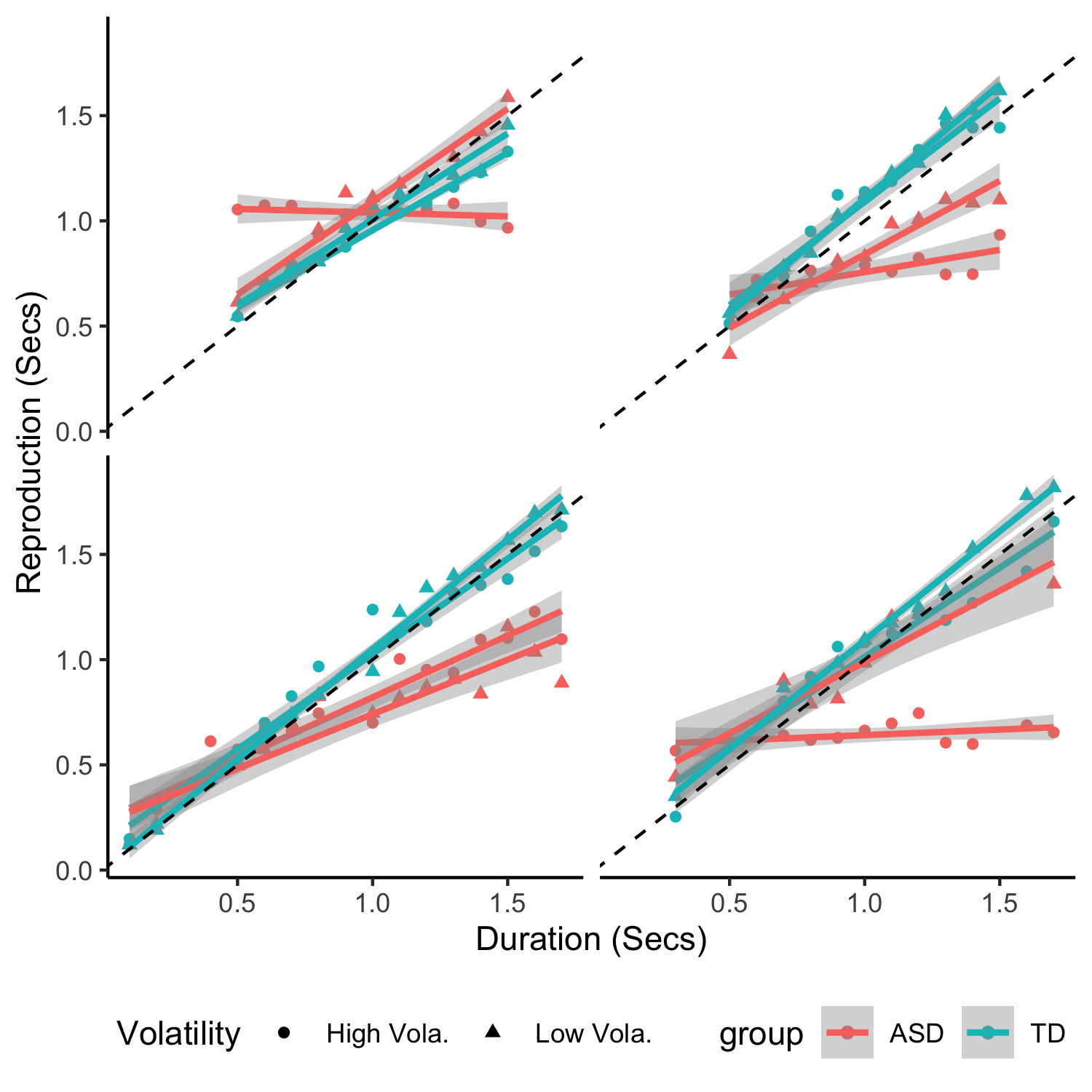
+Now let's visualize the outliers together with their matched pairs.
|
|
|
+
|
|
|
+```{r outliers}
|
|
|
+# ---- plot outliers ----
|
|
|
+fig_outlier = rawdata %>% ungroup() %>% filter(sequence %in% outlier_seq$sequence) %>%
|
|
|
+ filter(Reproduction > Duration/3, Reproduction < 3*Duration) %>%
|
|
|
+ group_by(sub, group,sequence, Volatility, Duration) %>%
|
|
|
+ summarise(mRep = mean(Reproduction), sdr=sd(Reproduction), n = n(),
|
|
|
+ se = sd(Reproduction)/sqrt(n-1)) %>% filter(n>5) %>% #approx. for linear regression without averaging first
|
|
|
+ ggplot(aes(Duration, mRep, color = group,
|
|
|
+ group = interaction(group, Volatility),
|
|
|
+ shape = Volatility, linetype = Volatility)) +
|
|
|
+ geom_point() + geom_smooth(method = 'lm', se = FALSE) +
|
|
|
+ facet_wrap(~sequence, ncol = 4) +
|
|
|
+ theme_classic() + theme(legend.pos = 'bottom') +
|
|
|
+ geom_abline(slope = 1, linetype = 3) +
|
|
|
+ xlab('Duration (Secs)') + ylab(' Reproduction (Secs)') +
|
|
|
+ theme(strip.background = element_blank(), strip.text.x = element_blank())
|
|
|
+fig_outlier
|
|
|
+if (saveFig){
|
|
|
+ ggsave("figures/fig_outlier.png", fig_outlier, width=5, height=5)
|
|
|
+ ggsave("figures/fig_outlier.pdf", fig_outlier, width=5, height=5)
|
|
|
+}
|
|
|
+```
|
|
|
+Mean slopes and related statistics:
|
|
|
+
|
|
|
+```{r}
|
|
|
+slopes %>% filter(sequence %in% outlier_seq$sequence) %>% arrange(group, Volatility)
|
|
|
+vslopes = slopes %>% filter(!(sequence %in% outlier_seq$sequence))
|
|
|
+
|
|
|
+# outliers
|
|
|
+oslopes = slopes %>% filter(sequence %in% outlier_seq$sequence)
|
|
|
+
|
|
|
+# ANOVA
|
|
|
+ezANOVA(data = oslopes, dv = ci,
|
|
|
+ wid = sub,
|
|
|
+ within = Volatility,
|
|
|
+ between = group)
|
|
|
+
|
|
|
+```
|
|
|
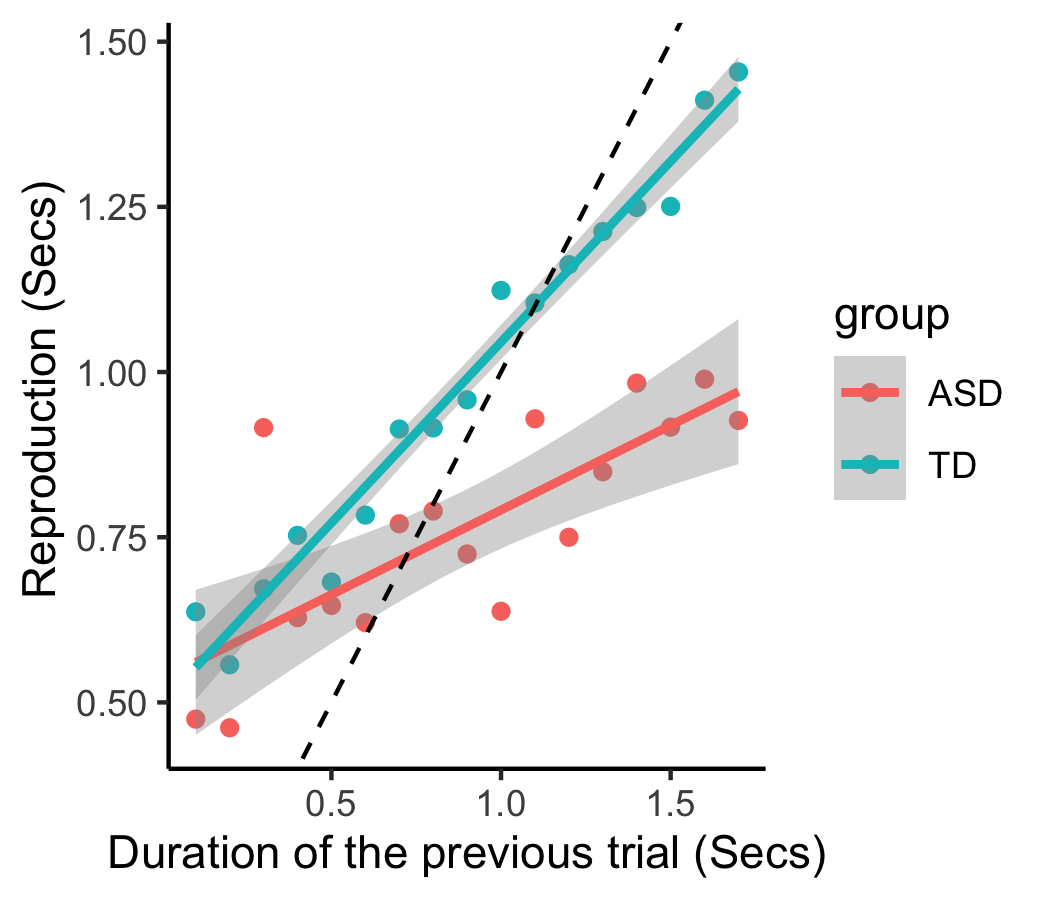
+### Outliers and sequential dependence
|
|
|
+
|
|
|
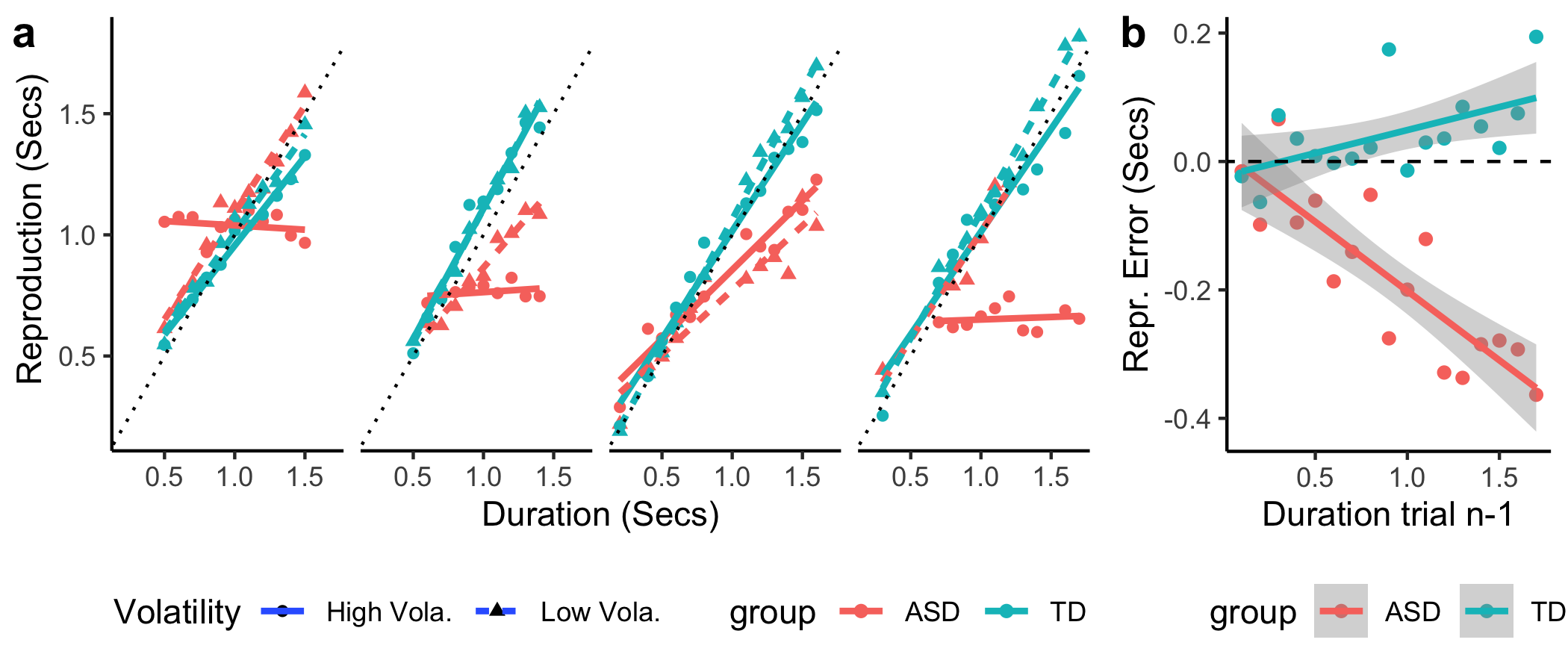
+Visualize the strong sequential dependence.
|
|
|
+
|
|
|
+```{r}
|
|
|
+fig_sdep31 = rawdata %>% filter(sequence %in% c(31) ) %>% # the extreme sequential dependence pair
|
|
|
+ mutate_at("preDuration", round, 1) %>%
|
|
|
+ group_by(sequence, group, preDuration) %>%
|
|
|
+ summarise(rep_err = mean(rep_err)) %>%
|
|
|
+ ggplot(aes(preDuration, rep_err, color = group) ) +
|
|
|
+ geom_point() + geom_smooth(method = 'lm') + theme_classic() +
|
|
|
+ geom_abline(slope = 0, linetype = 2) +
|
|
|
+# facet_wrap(~sequence) +
|
|
|
+ xlab('Duration trial n-1') + ylab('Repr. Error (Secs)') +
|
|
|
+ theme(strip.background = element_blank(), strip.text.x = element_blank(), legend.position = 'bottom')
|
|
|
+fig_sdep31
|
|
|
+
|
|
|
+fig_o = plot_grid(fig_outlier, fig_sdep31, nrow = 1, labels = c('a','b'), rel_widths = c(2.4,1))
|
|
|
+if (saveFig){
|
|
|
+ ggsave("figures/fig_o.png", fig_o, width=7, height=3)
|
|
|
+ ggsave("figures/fig_o.pdf", fig_o, width=7, height=3)
|
|
|
+
|
|
|
+}
|
|
|
+
|
|
|
+
|
|
|
+```
|
|
|
+
|
|
|
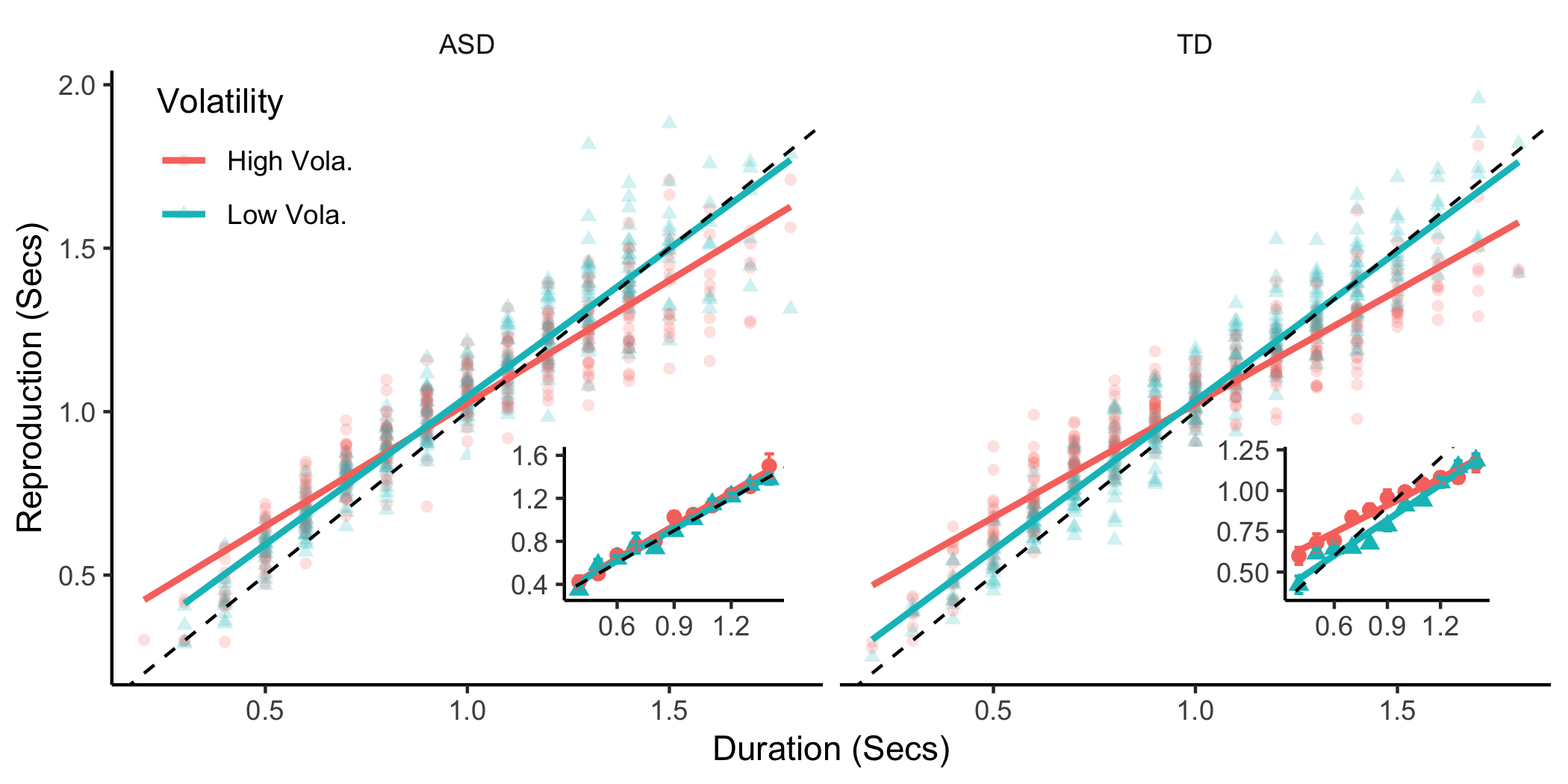
+## Typical reproduction performance
|
|
|
+
|
|
|
+And here are the two typical participants produced errors from sequence 12:
|
|
|
+```{r typical participants}
|
|
|
+# ---- reproduction figure - an example -----
|
|
|
+# mean analysis
|
|
|
+mrep = rawdata %>% ungroup() %>% filter(!(sequence %in% outlier_seq$sequence)) %>%
|
|
|
+ filter(Reproduction > Duration/3, Reproduction < 3*Duration) %>%
|
|
|
+ group_by(sub, group,Order, sequence, Volatility, Duration) %>%
|
|
|
+ summarise(mRep = mean(Reproduction), sdr=sd(Reproduction), n = n(),
|
|
|
+ se = sd(Reproduction)/sqrt(n-1)) %>% filter(n>3)
|
|
|
+
|
|
|
+# individual examples
|
|
|
+# asd
|
|
|
+fig_asd = mrep%>%
|
|
|
+ filter( sequence == '11', group == 'ASD') %>%
|
|
|
+ ggplot(aes(Duration, mRep, color = Volatility, group = Volatility, shape = Volatility)) +
|
|
|
+ geom_point(size = 2) +
|
|
|
+ #geom_line(aes(linetype = Volatility)) +
|
|
|
+ geom_smooth(method = 'lm', aes(fill = Volatility), se = FALSE) +
|
|
|
+ geom_errorbar(aes(ymin = mRep - se, ymax = mRep +se), width = 0.05) +
|
|
|
+ theme_classic() + theme(strip.background = element_blank()) +
|
|
|
+ geom_abline(slope = 1, linetype = 2) +
|
|
|
+ theme(legend.position = 'none', plot.margin = unit(c(0,0,0,0),'cm')) +
|
|
|
+ ylab('') + xlab('')
|
|
|
+
|
|
|
+#td
|
|
|
+fig_td = mrep%>%
|
|
|
+ filter( sequence == '11', group == 'TD') %>%
|
|
|
+ ggplot(aes(Duration, mRep, color = Volatility, group = Volatility, shape = Volatility)) +
|
|
|
+ geom_point(size = 2) +
|
|
|
+ geom_smooth(method = 'lm', aes(fill = Volatility), se = FALSE) +
|
|
|
+ geom_errorbar(aes(ymin = mRep - se, ymax = mRep +se), width = 0.05) +
|
|
|
+ theme_classic() + theme(strip.background = element_blank()) +
|
|
|
+ geom_abline(slope = 1, linetype = 2) +
|
|
|
+ theme(legend.position = 'none', plot.margin = unit(c(0,0,0,0),'cm')) +
|
|
|
+ ylab('') + xlab('')
|
|
|
+
|
|
|
+# group mean reproductions
|
|
|
+
|
|
|
+fig_repd_gr = mrep%>%
|
|
|
+ ggplot(aes(Duration, mRep, color = Volatility, group = Volatility, shape = Volatility)) +
|
|
|
+ geom_point(alpha = 0.2) +
|
|
|
+ geom_smooth(method = 'lm', se = FALSE, aes(fill = Volatility)) +
|
|
|
+ theme_classic() + theme(strip.background = element_blank()) +
|
|
|
+ geom_abline(slope = 1, linetype = 2) +
|
|
|
+ facet_wrap(~group) + theme(legend.position = c(0.1,0.85)) +
|
|
|
+ xlab('Duration (Secs)') + ylab('Reproduction (Secs)')
|
|
|
+
|
|
|
+# plot individual example as inset.
|
|
|
+
|
|
|
+fig_mrep = ggdraw() + draw_plot(fig_repd_gr) +
|
|
|
+ draw_plot(fig_asd, x = 0.3, y = 0.13, width = .2, height = .3) +
|
|
|
+ draw_plot(fig_td, x = 0.75, y = 0.13, width = .2, height = .3)
|
|
|
+
|
|
|
+fig_mrep
|
|
|
+if(saveFig){
|
|
|
+ ggsave("figures/fig_reproduction.png", fig_mrep, width=7, height=3.5)
|
|
|
+ ggsave("figures/fig_reproduction.pdf", fig_mrep, width=7, height=3.5)
|
|
|
+}
|
|
|
+```
|
|
|
+
|
|
|
+As we can see from the patterns above. The ASD participant produced relative flat errors, while the TD participant showed a strong central tendency effect (shorts being overestimated and longs being underestimated).
|
|
|
+
|
|
|
+
|
|
|
+### Visulize CTE and sequential dependence
|
|
|
+
|
|
|
+Let's visualize the biases (central tendency and serial dependence) for two groups (ASD vs. TD)
|
|
|
+
|
|
|
+```{r plot_biases}
|
|
|
+pd = position_dodge(width = 0.05)
|
|
|
+
|
|
|
+# plot CTI and SI together
|
|
|
+fig_biases = vslopes%>%
|
|
|
+ group_by(group, Volatility, Order) %>%
|
|
|
+ summarise(msi = mean(si), n = n(), se_si = sd(si)/sqrt(n),
|
|
|
+ mci = mean(ci), se_ci = sd(ci)/sqrt(n)) %>%
|
|
|
+ ggplot(aes(msi, mci, color = group, shape = Volatility,
|
|
|
+ group=interaction(Order, group))) +
|
|
|
+ geom_hline(yintercept = 0, color = 'gray', linetype = 'dashed') +
|
|
|
+ geom_vline(xintercept = 0, color = 'gray', linetype = 'dashed') +
|
|
|
+ geom_point(size = 2) +
|
|
|
+ geom_line(aes(linetype = Order)) +
|
|
|
+ geom_errorbar(aes(ymin = mci - se_ci, ymax = mci + se_ci), width = 0.01 ) +
|
|
|
+ geom_errorbarh(aes(xmin = msi - se_si, xmax = msi + se_si), height = 0.01) +
|
|
|
+ xlab('Serial Dependence') + ylab('Central Tendency') +
|
|
|
+ scale_y_continuous(labels = scales::percent) +
|
|
|
+ scale_x_continuous(labels = scales::percent) +
|
|
|
+ guides(color = guide_legend(title = 'Group'),
|
|
|
+ linetype = guide_legend(title = 'Volatility Order'),
|
|
|
+ ) +
|
|
|
+ theme_classic() +
|
|
|
+ theme(legend.position = 'bottom')
|
|
|
+fig_biases
|
|
|
+if (saveFig){
|
|
|
+ ggsave("figures/fig_biases.png", fig_biases, width=5, height=4)
|
|
|
+ ggsave("figures/fig_biases.pdf", fig_biases, width=5, height=4)
|
|
|
+}
|
|
|
+
|
|
|
+
|
|
|
+```
|
|
|
+
|
|
|
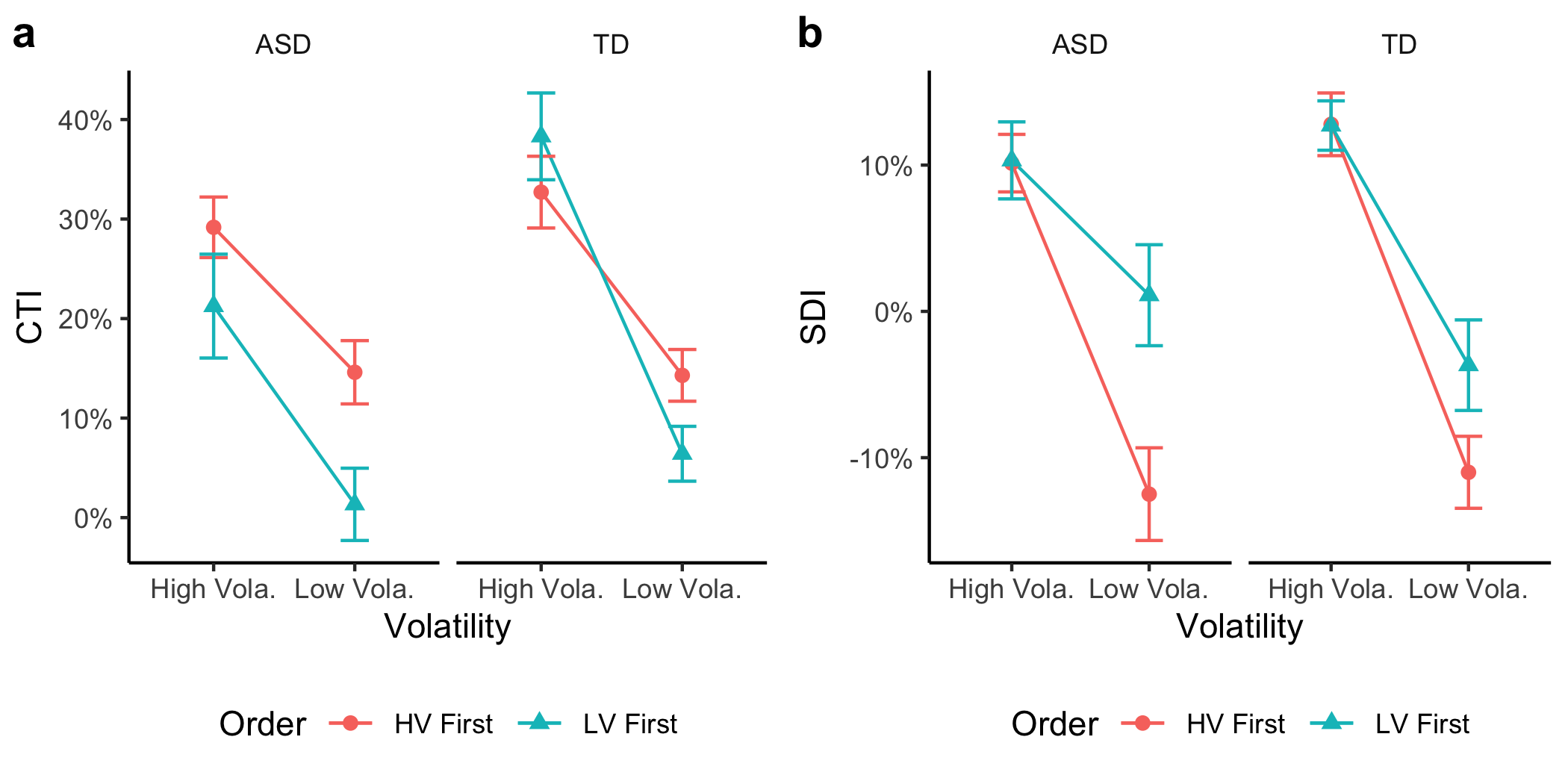
+By visual inspection, individuals with ASD exhibited less central tendency relative to their matched TD controls (the red lines below the cyan lines in the above figure), while the local serial dependence was relatively comparable between two groups except in the low volatility condition when that condition started first. Interestingly, the central tendency and serial dependence were similar for both groups when the high-volatility session started first (the solid lines), while they differed when the low-volatility session started first (the dashed lines).
|
|
|
+
|
|
|
+Given that the main difference was shown in CTE. We further plot the mean CTEs.
|
|
|
+
|
|
|
+```{r}
|
|
|
+#pd = position_dodge(width = 0.5)
|
|
|
+# separate plots for appendix
|
|
|
+fig_cti = vslopes %>%
|
|
|
+ group_by(group, Volatility, Order) %>%
|
|
|
+ summarise(mci = mean(ci), n = n(), se = sd(ci)/sqrt(n)) %>%
|
|
|
+ ggplot(aes(Volatility, mci, shape = Order, color = Order, group = Order)) +
|
|
|
+ geom_line() + geom_point(size= 2) +
|
|
|
+ #geom_bar(stat = 'identity', position = pd, width = 0.5) +
|
|
|
+ facet_wrap(~group)+
|
|
|
+ geom_errorbar(aes(ymin = mci - se, ymax = mci + se), width = 0.2) +
|
|
|
+ theme_classic() + theme(legend.position = 'bottom', strip.background = element_blank()) +
|
|
|
+ xlab('Volatility') + ylab('CTI') +
|
|
|
+ scale_y_continuous(labels = scales::percent) +
|
|
|
+ guides(color = guide_legend(title = 'Order'), fill = guide_legend(title = 'Order'))
|
|
|
+fig_cti
|
|
|
+
|
|
|
+```
|
|
|
+Let's do the sequential dependence as well.
|
|
|
+
|
|
|
+```{r}
|
|
|
+pd = position_dodge(width = 0.5)
|
|
|
+# separate plots for appendix
|
|
|
+fig_sdi = vslopes %>%
|
|
|
+ group_by(group, Volatility, Order) %>%
|
|
|
+ summarise(msi = mean(si), n = n(), se = sd(si)/sqrt(n)) %>%
|
|
|
+ ggplot(aes(Volatility, msi, shape = Order, color = Order, group = Order)) +
|
|
|
+ geom_line() + geom_point(size = 2) +
|
|
|
+ #geom_bar(stat = 'identity', position = pd, width = 0.5) +
|
|
|
+ facet_wrap(~group)+
|
|
|
+ geom_errorbar(aes(ymin = msi - se, ymax = msi + se), width = 0.2) +
|
|
|
+ theme_classic() + theme(legend.position = 'bottom', strip.background = element_blank()) +
|
|
|
+ xlab('Volatility') + ylab('SDI') +
|
|
|
+ scale_y_continuous(labels = scales::percent) +
|
|
|
+ guides(color = guide_legend(title = 'Order'), fill = guide_legend(title = 'Order'))
|
|
|
+fig_sdi
|
|
|
+fig3 = plot_grid(fig_cti, fig_sdi, nrow = 1, labels = c("a","b"))
|
|
|
+fig3
|
|
|
+if (saveFig){
|
|
|
+ ggsave('figures/fig3.pdf',fig3, width = 7, height = 3.5)
|
|
|
+ ggsave('figures/fig3.png',fig3, width = 7, height = 3.5)
|
|
|
+}
|
|
|
+
|
|
|
+```
|
|
|
+
|
|
|
+### Statistics
|
|
|
+
|
|
|
+1. Central tendency effect
|
|
|
+
|
|
|
+Average CTIs
|
|
|
+```{r}
|
|
|
+vslopes %>% group_by(group) %>% summarise(mcti = mean(ci))
|
|
|
+vslopes %>% group_by(Volatility) %>% summarise(mcti = mean(ci))
|
|
|
+vslopes %>% group_by(Order) %>% summarise(mcti = mean(ci))
|
|
|
+# calculate mean elevated CTIs between HV First vs. LV First
|
|
|
+vslopes %>% group_by(group, Volatility, Order) %>% summarise(mcti = mean(ci)) %>%
|
|
|
+ pivot_wider(names_from = Order, values_from = mcti) %>%
|
|
|
+ mutate(dCTI = `HV First` - `LV First`) %>%
|
|
|
+ group_by(group) %>% summarise(md = mean(dCTI))
|
|
|
+```
|
|
|
+
|
|
|
+
|
|
|
+```{r ANOVAs_cti}
|
|
|
+vslopes = as.data.frame(vslopes) # required by rstatix
|
|
|
+# ---- central tendency index----
|
|
|
+# repeated measures ANOVA on central tendency index
|
|
|
+anova1 = anova_test(data = vslopes, dv = ci,
|
|
|
+ wid = sub,
|
|
|
+ within = Volatility,
|
|
|
+ between = c(group, Order))
|
|
|
+anova1
|
|
|
+
|
|
|
+## separate for Volatility order
|
|
|
+anova1a = anova_test(data = vslopes %>% filter(group == 'ASD'),
|
|
|
+ dv = ci,
|
|
|
+ wid = sub,
|
|
|
+ within = Volatility,
|
|
|
+ between = Order)
|
|
|
+anova1a
|
|
|
+
|
|
|
+anova1b = anova_test(data = vslopes %>% filter(group == 'TD'),
|
|
|
+ dv = ci,
|
|
|
+ wid = sub,
|
|
|
+ within = Volatility,
|
|
|
+ between = Order)
|
|
|
+anova1b
|
|
|
+
|
|
|
+```
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+2. Bayes factor analysis for pair-wise comparison
|
|
|
+
|
|
|
+The above analysis showed that the main difference came from the central tendency. Here we further get the central tendency bias and Bayes factor analyses:
|
|
|
+```{r cti_bayes}
|
|
|
+
|
|
|
+# --- Bayes t-tests
|
|
|
+bftest = function(df){
|
|
|
+ df = as.data.frame(df)
|
|
|
+ # get the means
|
|
|
+ rdf = df%>% summarise(mci = mean(ci),
|
|
|
+ se_ci = sd(ci)/sqrt(n()),
|
|
|
+ msi = mean(si),
|
|
|
+ se_si = sd(si)/sqrt(n()))
|
|
|
+ rdf$ci_bf = ttestBF(df$ci, mu = 0) %>% extractBF() %>% .$bf
|
|
|
+ rdf$si_bf = ttestBF(df$si, mu = 0) %>% extractBF() %>% .$bf
|
|
|
+ return(rdf)
|
|
|
+}
|
|
|
+
|
|
|
+vslopes %>% group_by(group, Volatility, Order) %>% nest() %>%
|
|
|
+ mutate(bf = map(data, bftest)) %>% unnest(bf, .drop = TRUE)
|
|
|
+
|
|
|
+# group comparison for the low-vol-first, high-vol session
|
|
|
+vslopes %>% filter(Volatility == 'High Vola.', Order == 'LV First') %>% as.data.frame() ->v11
|
|
|
+t_test(data = v11, formula = ci ~ group)
|
|
|
+ttestBF(data = v11, formula = ci ~ group)
|
|
|
+
|
|
|
+vslopes %>% filter(Volatility == 'Low Vola.', Order == 'LV First') %>% as.data.frame() ->v12
|
|
|
+t_test(data = v12, formula = ci ~ group)
|
|
|
+ttestBF(data = v12, formula = ci ~ group)
|
|
|
+```
|
|
|
+
|
|
|
+
|
|
|
+3. ANOVA analyses for the serial dependence indices:
|
|
|
+
|
|
|
+```{r ANOVAs_sdi}
|
|
|
+# ---- Serial dependence index----
|
|
|
+anova2 = ezANOVA(data = vslopes, dv = si,
|
|
|
+ wid = sub,
|
|
|
+ within = .(Volatility),
|
|
|
+ between = .(group, Order))
|
|
|
+anova2$ANOVA
|
|
|
+
|
|
|
+# Bayes factors
|
|
|
+bf = anovaBF(si ~ Volatility + group + Order, data = vslopes, whichRandom = "sub")
|
|
|
+bayesfactor_inclusion(bf) #bayes inclusion values
|
|
|
+
|
|
|
+## separate for session order
|
|
|
+anova2a = ezANOVA(data = vslopes %>% filter(Order == 'LV First'),
|
|
|
+ dv = si,
|
|
|
+ wid = sub,
|
|
|
+ within = .(Volatility),
|
|
|
+ between = .(group))
|
|
|
+anova2a$ANOVA
|
|
|
+
|
|
|
+anova2b = ezANOVA(data = vslopes %>% filter(Order == 'HV First'),
|
|
|
+ dv = si,
|
|
|
+ wid = sub,
|
|
|
+ within = .(Volatility),
|
|
|
+ between = .(group))
|
|
|
+anova2b$ANOVA
|
|
|
+
|
|
|
+```
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+4. General biases
|
|
|
+
|
|
|
+Additionally we examined the general biases:
|
|
|
+```{r gBias}
|
|
|
+# ---- descriptive of general bias ----
|
|
|
+vslopes %>% group_by(group) %>% summarise(mg = mean(gBias), se = sd(gBias)/sqrt(n()))
|
|
|
+
|
|
|
+# ANOVA shows no differences
|
|
|
+anova2 = ezANOVA(data = vslopes, dv = gBias,
|
|
|
+ wid = sub,
|
|
|
+ within = .(Volatility),
|
|
|
+ between = .(group, Order))
|
|
|
+anova2$ANOVA
|
|
|
+
|
|
|
+bf = anovaBF(gBias ~ group + Volatility + Order,
|
|
|
+ data = as.data.frame(vslopes), whichRandom = "sub")
|
|
|
+bayesfactor_inclusion(bf) #bayes inclusion values
|
|
|
+
|
|
|
+
|
|
|
+```
|
|
|
+We then visualize the general biases
|
|
|
+```{r plotgBias}
|
|
|
+# --- general bias
|
|
|
+fig_bias = vslopes %>% group_by(group, Volatility, Order) %>%
|
|
|
+ summarise(mbias = mean(gBias), n = n(), se = sd(gBias)/sqrt(n)) %>%
|
|
|
+ ggplot(aes(Volatility, mbias, color = Order,linetype = group, group = interaction(Order, group), shape = group)) +
|
|
|
+ geom_point(size = 3, position = pd) +
|
|
|
+ geom_line(position = pd) +
|
|
|
+ geom_errorbar(aes(ymin = mbias - se, ymax = mbias + se), width = 0.2, position = pd) +
|
|
|
+ theme_classic() + theme(legend.position = 'bottom') + xlab('Volatility') +
|
|
|
+ ylab('Mean overestimation (ms)')
|
|
|
+fig_bias
|
|
|
+```
|
|
|
+
|
|
|
+There was no difference in two groups in general biases, although both groups were positive overestimated.
|
|
|
+
|
|
|
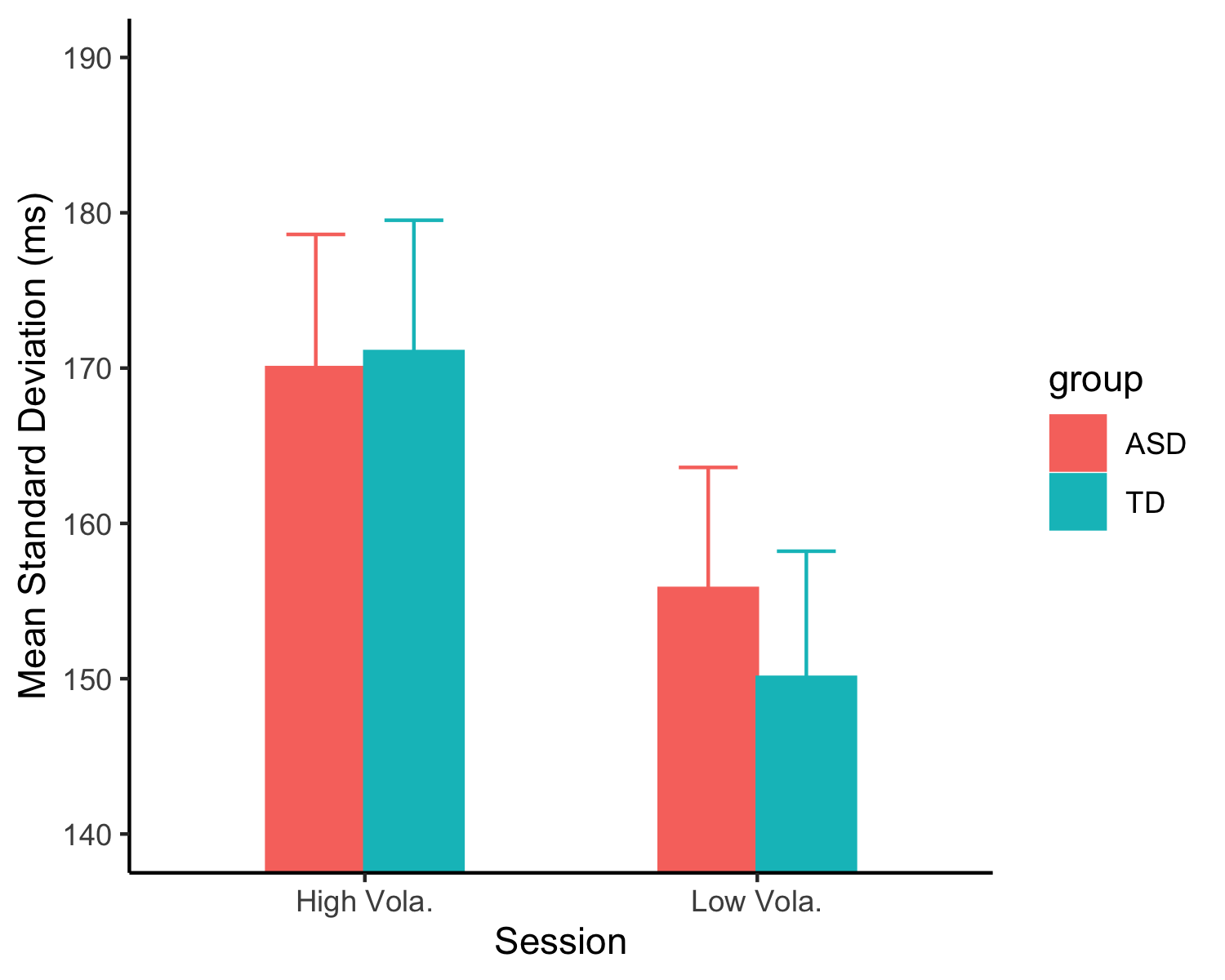
+Next we examined the reproduced variability:
|
|
|
+```{r rep_var}
|
|
|
+# ---- Reproduction variability -----
|
|
|
+msds_r <- mrep %>%
|
|
|
+ filter(n>5) %>%
|
|
|
+ group_by(group, Order, Volatility, sub) %>%
|
|
|
+ summarise(msd = mean(sdr), n=n(), msd_se = sd(sdr)/sqrt(n))
|
|
|
+
|
|
|
+
|
|
|
+sd_ANOVA <- ezANOVA(msds_r, dv=msd, wid=sub, between=.(group,Order), within=Volatility)
|
|
|
+sd_ANOVA$ANOVA
|
|
|
+
|
|
|
+mmsds_r <- msds_r %>% summarize(mmsd=mean(msd*1000), n = n(), se = sd(msd*1000)/sqrt(n))
|
|
|
+
|
|
|
+pd = position_dodge(width = 0.5)
|
|
|
+fig_sd <- ggplot(mmsds_r, aes(Volatility, mmsd, shape = Order, color = Order, group = Order)) +
|
|
|
+ geom_line() + geom_point() +
|
|
|
+ #geom_bar(stat = 'identity', position = pd, width = 0.5) +
|
|
|
+ geom_errorbar(aes(ymin = mmsd - se, ymax = mmsd + se), width = 0.3) +
|
|
|
+ facet_wrap(~group) +
|
|
|
+ ylab('Mean Standard Deviation (ms)') + xlab('Volatility') + theme_classic()
|
|
|
+# coord_cartesian(ylim = c(140, 200))
|
|
|
+fig_sd
|
|
|
+
|
|
|
+if(saveFig){
|
|
|
+ ggsave('figures/fig_sd.png', fig_sd, width=5, height=4)
|
|
|
+ ggsave('figures/fig_sd.pdf', fig_sd, width=5, height=4)
|
|
|
+}
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+```
|
|
|
+
|
|
|
+## Correlation analysis
|
|
|
+
|
|
|
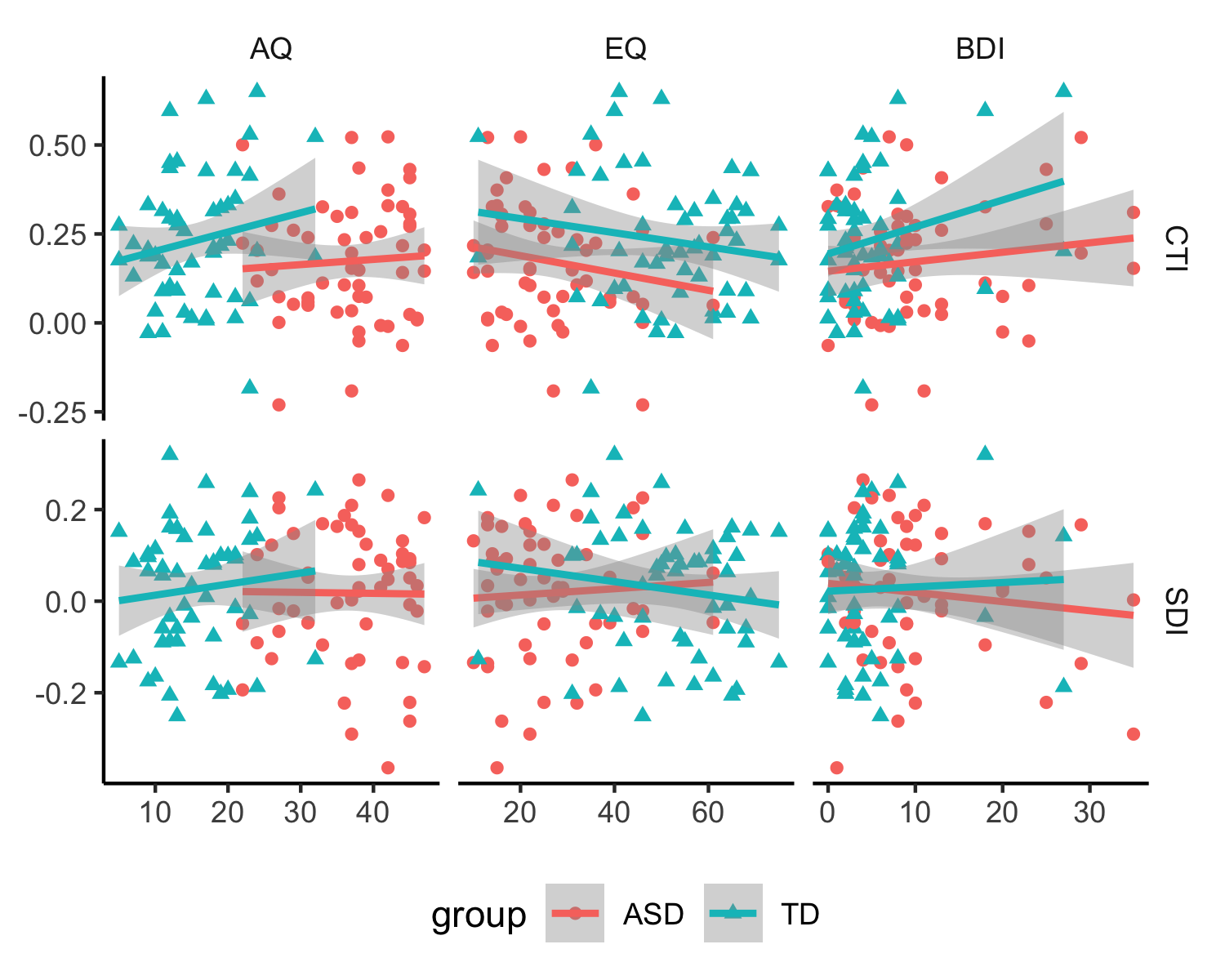
+Next we import individual participant ratings and do correlation analyses.
|
|
|
+
|
|
|
+```{r parinfo}
|
|
|
+pinfo = read.csv('data/parinfo.csv')
|
|
|
+
|
|
|
+# join with ctis, sdis
|
|
|
+res = left_join(vslopes, pinfo, by = c('group','sequence'))
|
|
|
+res$group = as.factor(res$group)
|
|
|
+
|
|
|
+# scatter plot to see any relations
|
|
|
+fig_corr = ggduo(res, c('AQ','EQ','BDI'), c('ci','si'), mapping = aes(color = group, shape = Order),
|
|
|
+ types = list(continuous = 'smooth_lm', se = FALSE),
|
|
|
+ showStrips = FALSE, legend = 3,
|
|
|
+ columnLabelsY = c('CTI','SDI')) +
|
|
|
+ theme_classic() + theme(legend.position = 'bottom', strip.background = element_blank())
|
|
|
+if(saveFig){
|
|
|
+ ggsave('figures/fig_corr.png', fig_corr, width=5, height=4)
|
|
|
+ ggsave('figures/fig_corr.pdf', fig_corr, width=5, height=4)
|
|
|
+}
|
|
|
+
|
|
|
+fig_corr
|
|
|
+```
|
|
|
+ Get linear regression out
|
|
|
+
|
|
|
+```{r}
|
|
|
+ci_AQ <- function(df){
|
|
|
+ lm(ci ~ AQ, data = df)
|
|
|
+}
|
|
|
+ci_EQ <- function(df){
|
|
|
+ lm(ci ~ EQ, data = df)
|
|
|
+}
|
|
|
+ci_BDI <- function(df){
|
|
|
+ lm(ci ~ BDI, data = df)
|
|
|
+}
|
|
|
+
|
|
|
+si_AQ <- function(df){
|
|
|
+ lm(si ~ AQ, data = df)
|
|
|
+}
|
|
|
+si_EQ <- function(df){
|
|
|
+ lm(si ~ EQ, data = df)
|
|
|
+}
|
|
|
+si_BDI <- function(df){
|
|
|
+ lm(si ~ BDI, data = df)
|
|
|
+}
|
|
|
+
|
|
|
+# regression
|
|
|
+reg_res <- res %>% group_by(Volatility, group, Order) %>%
|
|
|
+ nest() %>% # nested data
|
|
|
+ mutate(ci_AQ = map(data, ci_AQ), ci_EQ = map(data, ci_EQ),
|
|
|
+ ci_BDI = map(data, ci_BDI),
|
|
|
+ si_AQ = map(data, si_AQ), si_EQ = map(data, si_EQ),
|
|
|
+ si_BDI = map(data, si_BDI)) %>%
|
|
|
+ mutate(mci_AQ = map(ci_AQ, broom::tidy),
|
|
|
+ mci_EQ = map(ci_EQ, broom::tidy),
|
|
|
+ mci_BDI = map(ci_BDI, broom::tidy),
|
|
|
+ msi_AQ = map(si_AQ, broom::tidy),
|
|
|
+ msi_EQ = map(si_EQ, broom::tidy),
|
|
|
+ msi_BDI = map(si_BDI, broom::tidy) ) %>%
|
|
|
+ unnest(cols = c(mci_AQ, mci_EQ, mci_BDI, msi_AQ, msi_EQ, msi_BDI), names_repair = 'unique' , .drop = TRUE) %>%
|
|
|
+ select(-ci_AQ, -ci_BDI, -ci_EQ, -si_AQ, -si_EQ, -si_BDI, -data,
|
|
|
+ -starts_with('st')) %>%
|
|
|
+ filter(term == 'AQ') # remove intercept
|
|
|
+
|
|
|
+```
|
|
|
+
|
|
|
+Given there is no significant of slopes (after correction), but some difference in intercepts, we do general linear regression, without separating groups.
|
|
|
+
|
|
|
+```{r}
|
|
|
+reg_res2 <- res %>% ungroup() %>% group_by(Order, Volatility) %>%
|
|
|
+ nest() %>% # nested data
|
|
|
+ mutate(ci_AQ = map(data, ci_AQ), ci_EQ = map(data, ci_EQ),
|
|
|
+ ci_BDI = map(data, ci_BDI),
|
|
|
+ si_AQ = map(data, si_AQ), si_EQ = map(data, si_EQ),
|
|
|
+ si_BDI = map(data, si_BDI)) %>%
|
|
|
+ mutate(mci_AQ = map(ci_AQ, broom::tidy),
|
|
|
+ mci_EQ = map(ci_EQ, broom::tidy),
|
|
|
+ mci_BDI = map(ci_BDI, broom::tidy),
|
|
|
+ msi_AQ = map(si_AQ, broom::tidy),
|
|
|
+ msi_EQ = map(si_EQ, broom::tidy),
|
|
|
+ msi_BDI = map(si_BDI, broom::tidy) ) %>%
|
|
|
+ unnest(cols = c(mci_AQ, mci_EQ, mci_BDI, msi_AQ, msi_EQ, msi_BDI), names_repair = 'unique' , .drop = TRUE) %>%
|
|
|
+ select(-ci_AQ, -ci_BDI, -ci_EQ, -si_AQ, -si_EQ, -si_BDI, -data,
|
|
|
+ -starts_with('st')) %>%
|
|
|
+ filter(term == 'AQ') # remove intercept
|
|
|
+```
|
|
|
+Again, there is no significant of slopes.
|
|
|
+
|
|
|
+
|
|
|
+
|